TigerJython

2.9 REKURSIONEN

EINFÜHRUNG

Aus deiner frühen Kindheit kennst du möglicherweise die etwas unheimliche Geschichte vom Mann mit dem hohlen Zahn:

Äs isch ämal ä Ma gsi
dä het ä hohle Zahn gha
u i däm hohle Zahn isch äs Schachteli gsi
u i däm Schachteli isch äs Briefli gsi
u i däm Briefli isch gstande:
Äs isch ämal ä Ma gsi...

Es war einmal ein Mann,
der hatte einen hohlen Zahn,
in diesem hohlen Zahn befand sich eine Schachtel
in der Schachtel war ein Brief
in diesem Brief stand:
Es war einmal ein Mann...

Strukturen, die in ihrer Definition wieder sich selbst verwenden, nennt man rekursiv. Du kennst sicher die russische Matrjoschka: Eine Matrjoschka enthält in sich eine (etwas kleinere) Matrjoschka, diese enthält in sich eine Matrjoschka, diese enthält...

PROGRAMMIERKONZEPTE: Rekursion, Rekursionsverankerung, Indirekte Rekursion

REKURSIVER TREPPENBAU

Man stellt dir die Aufgabe eine Treppe mit 3 Stufen zu bauen. Statt zu sagen, dass du dreimal eine Stufe legen musst, könntest du aber auch sagen, dass eine Treppe aus 3 Stufen aus einer Stufe und einer Treppe aus 2 Stufen besteht, dann wiederum dass eine Treppe aus 2 Stufen aus einer Stufe und einer Treppe aus 1 Stufe besteht und dass eine Treppe aus 1 Stufe aus einer Stufe und einer Treppe aus 0 Stufen besteht, eine Treppe aus 0 Stufen aber nichts ist.

Diese Bauanleitung nennt man rekursiv, da in der Definition der Treppe mit 3 oder allgemein n Stufen die Treppe mit 2 oder allgemein n-1 Stufen verwendet wird. Als Programmcode:

def stairs(n):
    step()
    stairs(n-1)

Du wirst gleich die Turtle damit beauftragen, mit step() einen Treppenblock zu zeichnen, um dann mit dem Aufruf stairs(3) eine 3 stufige Treppe zu bauen. Aber warte noch, es fehlt doch die Angabe, dass beim Bau einer Treppe aus 0 Stufen gar nichts geschehen soll. Dies kannst du aber leicht mit einer if-Bedingung einbauen:

if n == 0:
   return

Die Anweisung return besagt, dass sie aufhören und zur vorherigen Arbeit zurückkehren kann. Dein Programm sieht nun so aus:

from gturtle import *

def stairs(n):
    if  n == 0:
        return
    step()
    stairs(n - 1)

def step():
    forward(50)
    right(90)
    forward(50)
    left(90)
    
makeTurtle()
fillToHorizontal(0)
stairs(3)

Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

MEMO

Unter Rekursionen versteht man ein fundamentales Lösungsverfahren in der Mathematik und Informatik, bei dem ein Problem derart gelöst wird, dass man es auf das gleiche, aber etwas vereinfachte Problem zurückführt. Wenn also f ein Funktion ist, die das Problem löst, so wird bei einer (direkten) Rekursion in der Definition von f wieder f verwendet [mehr... Bei der indirektion Rekursion werden in der Definition von f statt f selbst andere Funktionen verwendet, die f enthalten].

Auf den ersten Blick scheint es seltsam, dass man ein Problem derart lösen will, dass man die Lösung bereits voraussetzt. Dabei übersieht man aber einen wesentlichen Punkt: Es wird nicht genau dasselbe Problem zur Lösung verwendet, sondern eines, das der Lösung näher liegt. Dazu verwendet man einen meist ganzzahligen Ordnungsparameter n, den man f übergibt.

def f(n):
   ...

Bei der Wiederverwendung von f im Definitionsteil wird der Parameter verkleinert:

def f(n):
   ...
   f(n-1)
   ...

Eine so definierte Funktion würde sich aber endlos selbst aufrufen. Um dies zu verhindern, braucht man eine Abbruchbedingung, die man Rekursionsverankerung (oder Rekursionsbasis) nennt.

def f(n):
   if n == 0:
      return
   ...
   f(n - 1)
   ...

Mit dem Schüsselwort return wird die weitere Verarbeitung der Funktion abgebrochen. Man sagt auch, die Funktion kehre zurück.

DER PYTHAGORASBAUM

Mit rekursiven Algorithmen kannst du wunderbare Grafiken erzeugen. Du gehst von folgender Anleitung aus:

	Zeichne ausgehend von A ein Quadrat ABCD mit Basisseite AD
	Füge ein rechtwinkliges, gleichschenkliges BD1C Dreieck an der Seite BC an
	Zeichne den Baum erneut ausgehend von den Quadraten A1D1 und A2D2 als Basisseiten

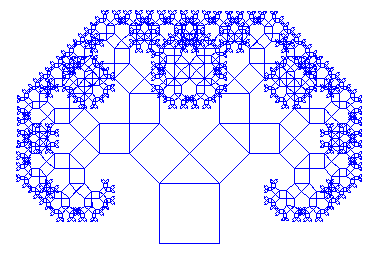
Es ist bekannt, dass die Umsetzung in ein rekursives Programm ungewohnt ist. Darum erhältst du hier eine ausführliche Anleitung, wie du vorgehen musst.

	Definiere einen Befehl square(s), mit dem die Turtle ein Quadrat mit der Seitenlänge s zeichnet und wieder in die Anfangsposition mit Anfangsblickrichtung zurückkehrt
	Definiere den Befehl tree(s), welcher einen Baum ausgehend von einem Quadrat der Seitenlänge s zeichnet. In der Definition darfst du tree() wieder verwenden. Wichtig: Nach dem Zeichnen des Baums ist die Turtle wieder in der Anfangsposition mit Anfangsblickrichtung. Du überlegst schrittweise, als ob du die Turtle wärst (das neu Hinzugefügte ist grau unterlegt).

Du zeichnest zuerst vom Punkt A aus ein Quadrat mit der Seitenlänge s:

def tree(s):
     square(s)

Du fährst zur Ecke B des Quadrats, drehst 45 Grad nach links und betrachtest dies als Startpunkt eines neuen Baums mit verkleinertem Parameter s1. Es gilt nach dem Satz von Pythagoras:

s₁ =

( s )/ √ 2

def tree(s):
   square(s)
   forward(s)
   s1 = s / math.sqrt(2)   
   left(45)
   tree(s1)

Da du ja voraussetzt, dass du nach dem Zeichnen des Baums wieder am Startpunkt mit der Startblickrichtung landest, befindest du dich wieder in B und schaust in Richtung B1. Du drehst dich um 90 Grad nach rechts und fährst die Strecke s1 vorwärts. Jetzt bist du im Punkt D1 und hast die Blickrichtung zu B2. Von hier aus zeichnest du den Baum erneut.

def tree(s):
   square(s)
   forward(s)
   s1 = s / math.sqrt(2)
   left(45)
   tree(s1)
   right(90)
   forward(s1)
   tree(s1)

Jetzt musst du nur noch an den Anfangsort A mit der Anfangsblickrichtung zurückkehren. Dazu bewegst du dich um s1 rückwärts, drehst dich um 45 Grad nach links und fährst um s rückwärts.

def tree(s):
   square(s)
   forward(s)
   s1 = s / math.sqrt(2)
   left(45)
   tree(s1)
   right(90)
   forward(s1)
   tree(s1)
   back(s1)
   left(45)
   back(s)

from gturtle import *
import math

def tree(s):
    if s < 2:
        return
    square(s)
    forward(s)
    s1 = s / math.sqrt(2)
    left(45)
    tree(s1)
    right(90)
    forward(s1)
    tree(s1)
    back(s1)
    left(45)
    back(s)

def square(s):
    repeat 4:
        forward(s)
        right(90)

makeTurtle()
ht()
setPos(-50, -200)
tree(100)

Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

MEMO

Bei vielen rekursiv definierten Figuren ist es wichtig, dass die Turtle wieder an ihren Anfangsort mit der Anfangsblickrichtung zurückkehrt.

AUFGABEN

Wo liegt der wesentliche Unterschied der beiden Programme? Untersuche insbesondere Ort und Richtung der Turtle nach Programmende. Warum nennt man figA eine "Last Line Recursion" und figB eine "First Line Recursion"?

from gturtle import *

def  figA(s):
   if s > 200:
      return
   forward(s)
   right(90)
   figA(s + 10)

makeTurtle()
figA(100)

from gturtle import *

def  figB(s):
   if s > 200:
      return
   figB(s + 10)
   forward(s)
   right(90)

makeTurtle()
figB(100)

Ein bekannter Graf ist der vollständige binäre Baum. Er sieht für eine bestimmte Rekursionstiefe wie nebenstehend gezeigt aus. Schreibe eine rekursive Funktion tree(s), die den Baum mit der "Stammlänge" s zeichnet.

Zeichne die nebenstehende Sternfigur.
Definiere dazu die rekursive Funktion star(s), welche die Turtle einen Stern mit der "Dimension" s zeichnen lässt (s ist die Distanz vom Zentrum der Sternfigur zum Zentrum in der nächsten Generation). s wird von Generation zu Generation auf 1/3 reduziert. Rufe stern(180) auf und verankere die Rekursion, dass sie bei s < 20 abbricht. Wenn du hideTurtle() verwendest, wird die Turtle viel schneller zeichnen.

4*.

Du wirst einen Baum zeichnen, der schon fast wie ein echter Baum aussieht. Definiere dazu die rekursive Funktion treeFractal(s), mit der "Stammlänge" s, die wie folgt aufgebaut ist:

	Verankere die Rekursion bei einer Stammlänge kleiner als 5.
	Speichere dir zuerst mit getX() und getY() die aktuelle x- und y-Koordinaten der Turtle, sowie mit heading() ihre Blickrichtung, damit du einfach zurückkehren kannst
	Jetzt fährst um s/3 nach vorne, drehst dich um 30 Grad nach links und zeichnest den Baum mit der Stammlänge 2*s/3
	Du drehst dich um 30 Grad nach rechts, fährst s/6 nach vorn, drehst 25 Grad nach rechts und zeichnest den Baum mit der Stammlänge s/2
	Du drehst dich um weitere 25 Grad nach rechts, fährst um s/3 nach vorn, drehst um 25 Grad nach rechts und zeichnest den Baum noch einmal mit der Stammlänge s/2
	Du kehrst mit setPos() und heading() wieder in die Anfangslage mit der Anfangsposition zurück