deutsch     english    français     Imprimer

 

10.2 PROBLÈMES INSOLUBLES

 

 

INTRODUCTION

 

ILe nombre de problèmes qu’il est possible de résoudre par ordinateur est de plus en plus important. Dans ce chapitre, nous serons cependant confrontés à des problèmes qui se laissent formuler très aisément mais qui ne pourront sans doute jamais être résolus de manière algorithmique. Il y a de fortes chances pour que cela ne change pas malgré la croissance rapide de la puissance de traitement des ordinateurs et toutes les recherches scientifiques qui se consacrent à ces problèmes.

CONCEPTS DE PROGRAMMATION:
Problèmes insolubles, problème de la somme des sous-ensembles, méthode d’énumération, explosion combinatoire, ordre polynomial, problème indécidable

 

 

PROBLÈMES INSOLUBLES

 

Il reste encore aujourd’hui de nombreux problèmes non résolus alors même qu’ils sont très faciles à énoncer et qu’ils présentent un intérêt conséquent en pratique. L’un de ces problèmes, nommé le problème de la somme des sous-ensembles, peut être formulé de la manière suivante [plus...Le problème de la somme des sous-ensembles est un cas particulier du problème du sac à dos]:

Vous disposez dans votre porte-monnaie d’un certain nombre de pièces de monnaie et vous devez payer une certaine somme à un automate sans qu’il ne rende la monnaie. Cela est-il possible avec les pièces dont vous disposez et, si oui, quelles sont les pièces qu’il faut utiliser?

Notre premier programme nous permettra d’apprendre à gérer les pièces de monnaie. Le programme commence par stocker dans la liste coins le nom des pièces d’Euro de valeur 1, 2, 5, 10, 20 et 50 centimes. La fonction value() retourne la valeur de la pièce. Le porte-monnaie est modélisé par une liste (ou un tuple) moneybag contenant le nom des pièces présentes dans le porte-monnaie. La fonction getSum(moneybag) retourne la valeur totale de l’ensemble des pièces se trouvant dans le portemonnaie.

Dans un premier temps, prenons un porte-monnaie contenant exactement un exemplaire de chaque pièce. Le programme construit alors toutes les différentes combinaisons de pièces comportant 1, 2, 3, 4, 5 ou 6 pièces et les affiche dans une fenêtre JGameGrid. Pour ce faire, la fonction showMoneybag(moneybag, y) crée une instance de la classe Actor pour chaque pièce de monnaie du porte-monnaie et l’affiche dans la fenêtre sur la rangée (ligne) y.

 

   
from gamegrid import *
import itertools

coins = ["one", "two", "five", "ten", "twenty", "fifty"] 

def value(coin):
    if coin == "one":
        return 1
    if coin == "two":
        return 2
    if coin == "five":
        return 5
    if coin == "ten":
        return 10
    if coin == "twenty":
        return 20
    if coin == "fifty":
        return 50
    return 0

def getSum(moneybag):
    count = 0
    for coin in moneybag:
        count += value(coin)
    return count

def showMoneybag(moneybag, y):
    x = 0
    for coin in moneybag:
        loc = Location(x, y)
        removeActor(getOneActorAt(loc))
        coinActor = Actor("sprites/" + coin + "cent.png")
        addActor(coinActor, loc)
        x += 1
    addActor(TextActor(str(getSum(moneybag))), Location(x, y))    

makeGameGrid(8, 20, 40, False)
setBgColor(Color.white)
show()

n = 6 
k = 1
while k <= n:
    combinations = list(itertools.combinations(coins, k))
    setTitle("(n, k) = (" + str(n) + ", " + str(k) + ") nb = "
    + str(len(combinations)))
    y = 0
    for moneybag in combinations:
        showMoneybag(moneybag, y)
        y += 1
    getKeyCodeWait()
    removeAllActors()
    k += 1
Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

 

 

MEMENTO

 

La fonction combinations() du module itertools permet d’obtenir facilement toutes les combinaisons de k éléments que l’on peut fabriquer à partir des éléments d’une liste de longueur n. Il est cependant nécessaire de convertir la valeur de retour en une liste pour en extraire une à une chacune des combinaisons sous forme de tuple.

Les combinaisons ainsi obtenues sont ordonnées selon un ordre naturel semblable à celui que l’on obtiendrait si l’on avait fait le travail à la main. On peut calculer exactement le nombre de combinaisons de longueur k issues d’un ensemble de n éléments grâce au fameux coefficient binomial :

où n! est la factorielle de n, à savoir le produit de tous les nombres de 1 à n. Pour n=6, on pourrait avoir 6, 15, 20, 15, 6, 1 et, de ce fait, un total de 63 combinaisons

 

 

On peut résoudre le problème de la somme des sous-ensembles du porte-monnaie de la manière suivante : il faut déterminer toutes les combinaisons possibles de pièces de monnaies présentes dans le porte-monnaie et tester si la somme de ce sous-ensemble correspond à la somme désirée.

Cette méthode d’énumération n’est probablement pas la plus efficace que l’on puisse imaginer mais elle a le mérite d’être correcte et de fournir toutes les solutions possibles. Pour un porte-monnaie qui contient 3 pièces de 1 ct, 1 pièce de 2 ct, 2 pièces de 5 ct, 4 pièces de 10 ct, 2 pièces de 20 ct et 3 pièces de 50 ct (15 pièces en tout), il serait déjà difficile de trouver la solution à la main par énumération. On n’écrit que les combinaisons dont la somme totale se monte à un Euro .

 

   



from gamegrid import *
import itertools

coins = ["one", "one", "one", "two", "five", "five", 
         "ten", "ten", "ten", "ten", "twenty", "twenty", 
         "fifty", "fifty", "fifty"] 

def value(coin):
    if coin == "one":
        return 1
    if coin == "two":
        return 2
    if coin == "five":
        return 5
    if coin == "ten":
        return 10
    if coin == "twenty":
        return 20
    if coin == "fifty":
        return 50
    return 0

def getSum(moneybag):
    count = 0
    for coin in moneybag:
        count += value(coin)
    return count

def showMoneybag(moneybag, y):
    x = 0
    for coin in moneybag:
        loc = Location(x, y)
        removeActor(getOneActorAt(loc))
        coinActor = Actor("sprites/" + coin + "cent.png")
        addActor(coinActor, loc)
        x += 1
    addActor(TextActor(str(getSum(moneybag))), Location(x, y))

makeGameGrid(15, 20, 40, False)
setBgColor(Color.white)
show()

target = 100

k = 1
result = []
count = 0
while k <= len(coins):
    combinations = tuple(itertools.combinations(coins, k))
    nb = len(combinations)
    for moneybag in combinations:
        count += 1
        count = getSum(moneybag)
        if count == target:
            if not moneybag in result:
               result.append(moneybag)
    k += 1

y = 0
for moneybag in result:
    showMoneybag(moneybag, y)
    y += 1
setTitle("Step: " + str(count) + ". number of solutions for the count  "
          + str(target) + ": " + str(len(result)))
Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

 

 

MEMENTO

 

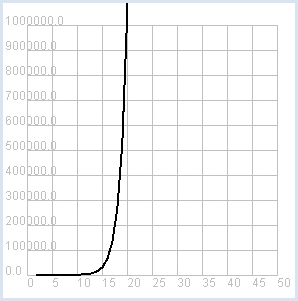
Pour un nombre restreint de 15 pièces de monnaie, une méthode par énumération nécessite déjà la bagatelle de 32'767 étapes pour résoudre le problème de la somme des sous-ensembles.

On peut être tout fou d’être en mesure de développer un programme qui s’acquittera de cette tâche très rapidement mais on déchantera rapidement lorsque l’on sera confronté à un nombre légèrement supérieur de pièces de monnaies, par exemple 50 ou 100. Si l’on compte le nombre de pas nécessaires pour un porte-monnaie comptant n pièces et que l’on affiche ce résultat dans un graphique lorsque n augmente, on constate qu’il y a une véritable explosion combinatoire pour n=20 qui dépasse tout ce qui est imaginable avec les ordinateurs actuels. plus... Le livre Sieben Wundern der Informatik de Hromkovic présente d’autres problèmes qui poussent
les ordinateurs dans leur ultime retranchement"].

 

 

   

from gpanel import *
from math import factorial

z = 100 

def nbCombi(n, k):
    return factorial(n) / factorial(k) / factorial(n - k)

makeGPanel(-5, 55, -1e5, 1.1e6)
drawGrid(0, 50, 0, 1e6, "gray")
setColor("black")
lineWidth(2)
for n in range(2, z + 1):
    count = 0
    for k in range(1, n):
        count += nbCombi(n, k)
    print "n =", n, ", nb =", count
    if n == 2:
        move(n, count)
    else:
        draw(n, count)
print "Runtime with 10^9 operations per second:", count / 3.142e16, "years" 
print "or:", int(count / 2e20), "times the age of the universe"
Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)


 

MEMENTO

 

Si l’on utilise la méthode de l’énumération, le problème de la somme des sous-ensembles est déjà insoluble pour un nombre relativement faible d’éléments, alors même que l’algorithme de résolution est connu. Il reste encore à savoir s’il n’existerait pas des algorithmes qualitativement très supérieurs dont la complexité temporelle serait une puissance de n (complexité polynomiale) comme le sont les algorithmes de tri vus dans le chapitre précédent. Malheureusement, personne n’a jusqu’à présent trouvé un tel algorithme pour le problème de la somme des sous-ensembles et on part en général du principe qu’il n’y en pas. Par contre, il n’existe pas non plus de preuve qu’un tel algorithme n’existe pas.

On sait du moins de l’informatique théorique qu’il existe de nombreux problèmes de la même classe de difficulté et que si l’on trouve une méthode efficace de résolution pour l’un de ces problèmes, alors tous les problèmes de cette difficulté sont d’emblée résolubles à partir de cette méthode [plus... On dit de cette classe de problèmes qu’il sont NP-complets].

 

 

PROBLÈMES INDÉCIDABLES

 

Les limites de l’esprit humain et de la technologie informatique se révèlent également dans un contexte différent de celui de la théorie de la complexité. Le mathématicien et théoricien des nombres Lothar Collatz s’est penché sur certaines suites de nombres et a formulé en 1939 la question suivante:

Prenons une suite de nombres dont le terme initial est un nombre naturel quelconque dont les termes consécutifs sont construits à partir des règles de récurrence suivantes :

  • Si n est pair, diviser n par 2 (qui est à nouveau un nombre naturel)
  • Si n est impair, prendre le nombre 3n+1 (qui est forcément un nombre pair)

Question : Cette suite converge-t-elle toujours vers 1 quel que soit le terme initial n?

Collatz ainsi que de nombreux autres théoriciens des nombres et chercheurs en informatique ont tenté de répondre à cette question puisque même les plus puissants ordinateurs de la planète obtiennent sans arrêt des suites qui atteignent le nombre 1 (les suites ne convergent pas car elles répètent de manière infinie la séquence 4, 2, 1).

Il apparaît donc vraisemblable que le théorème suivant soit vérifié:

Pour tout terme initial n, la suite 3n+1 atteint le nombre 1 en un nombre fini d’étapes.

On peut faire soi-même l’expérience et parcourir la suite (3n+1) à l’aide d’un programme informatique pour un nombre initial n quelconque. 

from gpanel import *

def collatz(n):
    while n != 1:
        if n % 2 == 0:
            n = n // 2
        else:
            n = 3 * n + 1
        print n,
    print "Result 1"
while True:
    n = inputInt("Enter a start number:") 
    collatz(n)
Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

 
 

MEMENTO

 

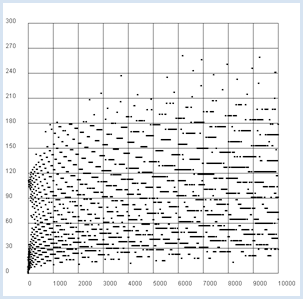
En Python, il est même possible de calculer les termes de la suite 3n+1 pour un terme initial très grand. Selon le théorème précédent, la suite en question va toujours finir, après un nombre suffisamment grand mais fini d’itérations, par tomber sur le nombre 1. Évidemment, ceci ne constitue aucunement une preuve de la question posée par Collatz.

 

 

Il est intéressant et même très esthétique de représenter la longueur de la suite 3n+1 en fonction du terme initial de la suite. On remarque que cette longueur fluctue considérablement. Pour ce faire, il faut supprimer l’affichage dans la console des termes de la suite au sein de la fonction collatz() et se contenter de retourner le nombre d’étapes jusqu’à ce que l’on tombe sur 1.

  

 

from gpanel import *

def collatz(n):
    nb = 0
    while n != 1:
        nb += 1
        if n % 2 == 0:
            n = n // 2
        else:
            n = 3 * n + 1
    return nb             

z = 10000 # max n
yval = [0] * (z + 1)
for n in range(1, z + 1):
    yval[n] = collatz(n)
ymax = (max(yval) // 100  + 1) * 100

makeGPanel(-0.1 * z, 1.1 * z, -0.1 * ymax, 1.1 * ymax)
title("Collatz Assumption")
drawGrid(0, z, 0, ymax, "gray")

for x in range(1, z + 1):
    move(x, yval[x])
    fillCircle(z / 200)
Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

 

 

 

MEMENTO

 

L’hypothèse de Collatz est un problème vraiment très difficile. En supposant que l’hypothèse soit vraie, il n’est pas possible de la prouver en effectuant un très grand nombre de tests par ordinateurs pour des nombres n toujours plus grands. Il est même possible que l’hypothèse soit vraie mais qu’il ne soit pas possible de prouver sa véracité. En 1931, le mathématicien Kurt Gödel a montré avec son théorème d’incomplétude qu’il peut exister des affirmations qui sont vraies à l’intérieur d’une théorie mais dont la véracité ne peut pas être prouvée.

Le problème de Collatz peut également être formulé comme un problème de décision:

Un algorithme qui calcule les termes de la suite 3n+1 et qui s’arrête à 1 s’arrête-t-il vraiment pour tous les termes initiaux possibles?

On peut essayer de résoudre cette question par ordinateur. Malheureusement, cette tentative est probablement complètement vaine elle aussi car le grand mathématicien Alan Turing a déjà prouvé avec son problème de l’arrêt (Halting Problem en anglais) qu’il n’existera jamais un algorithme général permettant de décider si un programme va s’arrêter quelles que soient les données qu’on lui fournit en entrée.

Il se peut donc que l’hypothèse de Collatz soit correcte mais qu’elle constitue un problème indécidable.