8.9 GROUP DYNAMICS
![]()
INTRODUCTION |
Systems with many partners that interact with each other are widely used. Computer programs can often simulate such systems with surprisingly little effort, since the computer can store anywhere from thousands to millions of single individual states and temporally track them. However, if we deal with atomic many-body systems with a numbers of particles in the order of 1023, computers reach their limits. To simulate such systems, we need to use simplifying procedures, such as dividing the system into several larger cells. Examples for this include the simulation of Earth's atmosphere for weather forecast and the prediction of long-term climate change. |
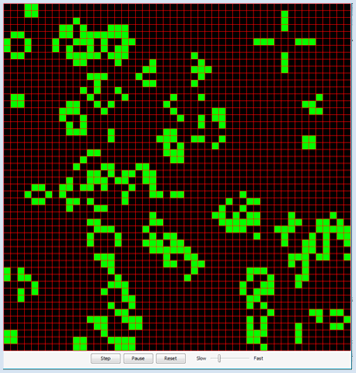
CONWAY'S GAME OF LIFE |
When transitioning to the next generation, the current state is saved and the following state of each cell is determined based on its 8 nearest neighbors by the following four transition rules:
The cell structure of GameGrid is ideal for implementing the game. You use a two-dimensional list a[x][y] for the population, where the value 0 is a dead cell and 1 is a living cell. The simulation cycle is regarded as a generation cycle, and the current population from the list a is copied into the new population b in the callback onAct() and will finally be regarded as the current list. You choose 1,000 random living cells in the callback onReset(), which is called by clicking on the reset button. In order to activate the callbacks, you have to register them with registerAct() and registerNavigation().. from gamegrid import * def onReset(): for x in range(s): for y in range(s): a[x][y] = 0 # All cells dead for n in range(z): loc = getRandomEmptyLocation() a[loc.x][loc.y] = 1 showPopulation() def showPopulation(): for x in range(s): for y in range(s): loc = Location(x, y) if a[x][y] == 1: getBg().fillCell(loc, Color.green, False) else: getBg().fillCell(loc, Color.black, False) refresh() def getNumberOfNeighbours(x, y): nb = 0 for i in range(max(0, x - 1), min(s, x + 2)): for k in range(max(0, y - 1), min(s, y + 2)): if not (i == x and k == y): if a[i][k] == 1: nb = nb + 1 return nb def onAct(): global a # Don't use the current, but a new population b = [[0 for x in range(s)] for y in range(s)] for x in range(s): for y in range(s): nb = getNumberOfNeighbours(x, y) if a[x][y] == 1: # living cell if nb < 2: b[x][y] = 0 elif nb > 3: b[x][y] = 0 else: b[x][y] = 1 else: # dead cell if nb == 3: b[x][y] = 1 else: b[x][y] = 0 a = b # Use new population as current showPopulation() # =================== global section ================== s = 50 # Number of cells in each direction z = 1000 # Size of population at start a = [[0 for x in range(s)] for y in range(s)] makeGameGrid(s, s, 800 // s, Color.red) registerAct(onAct) registerNavigation(resetted = onReset) setTitle("Conway's Game Of Life") onReset() show() |
MEMO |
The Game of Life is an example of a cellular automaton, consisting of grid cells that interact with each other. They are perfectly suited to study the behavior of complex natural systems. Some examples are:
In 2002, Stefan Wolfram, the scientist and chief developer of Mathematica pointed out in his well known book "A New Kind of Science" that such systems can be investigated with simple programs. With computer simulations, we are at the beginning of a new era of gaining scientific knowledge. During the initialization of the two-dimensional list, a special Python syntax called list comprehension is used (see addional material). |
SWARMING BEHAVIOR |
As you know from your daily life, large groups of living beings often have the tendency to team up together in groups. This can be observed particularly well in birds, fish, and insects. A group of demonstrating people also shows this "swarming behavior". On the one hand, outside (global) influences play a role in the formation of a swarm, but the interaction between partners in their close surroundings (local influences) also play a role. In 1986 Craig Reynolds showed that the following three rules lead to a swarm formation between individuals (he called them Boids):
To implement this, you use JGameGrid again in order to keep the effort of the animation low. It helps to use a grid with pixel sizes and to specify the position, velocity, and acceleration of the actors with float vectors from the class GGVector. In each simulation period you first determine the new acceleration vector according to the three rules using setAcceleration(). This results in the new velocity and position vectors
Since the absolute time scale is insignificant, you can set the time increment to dt = 1. Applying the separation rule not only leads to a rejection between the closely flying birds, but also between them and obstacles (in this case, trees). You have to particularly deal with the edge of the flying area (the wall). For this, there are various possibilities to choose from. You could, for example, use a toroidal topology, where the birds leaving the area on one side enter it again on the other. In this case, the birds are simply forced to turn around at the edge. from gamegrid import * import math from random import randint # =================== class Tree ======================= class Tree(Actor): def __init__(self): Actor.__init__(self, "sprites/tree1.png") # =================== class Bird ======================= class Bird(Actor): def __init__(self): Actor.__init__(self, True, "sprites/arrow1.png") self.r = GGVector(0, 0) # Position self.v = GGVector(0, 0) # Velocity self.a = GGVector(0, 0) # Acceleration # Called when actor is added to gamegrid def reset(self): self.r.x = self.getX() self.r.y = self.getY() self.v.x = startVelocity * math.cos(math.radians(self.getDirection())) self.v.y = startVelocity * math.sin(math.radians(self.getDirection())) # ----------- cohesion --------------- def cohesion(self, distance): return self.getCenterOfMass(distance).sub(self.r) # ----------- alignment -------------- def alignment(self, distance): align = self.getAverageVelocity(distance) align = align.sub(self.v) return align # ----------- separation ------------- def separation(self, distance): repulse = GGVector() # ------ from birds ------ for p in birdPositions: dist = p.sub(self.r) d = dist.magnitude() if d < distance and d != 0: repulse = repulse.add(dist.mult((d - distance) / d)) # ------ from trees ------ trees = self.gameGrid.getActors(Tree) for actor in trees: p = GGVector(actor.getX(), actor.getY()) dist = p.sub(self.r) d = dist.magnitude() if d < distance and d != 0: repulse = repulse.add(dist.mult((d - distance) / d)) return repulse # ----------- wall interaction ------- def wallInteraction(self): width = self.gameGrid.getWidth() height = self.gameGrid.getHeight() acc = GGVector() if self.r.x < wallDist: distFactor = (wallDist - self.r.x) / wallDist acc = GGVector(wallWeight * distFactor, 0) if width - self.r.x < wallDist: distFactor = ((width - self.r.x) - wallDist) / wallDist acc = GGVector(wallWeight * distFactor, 0) if self.r.y < wallDist: distFactor = (wallDist - self.r.y) / wallDist acc = GGVector(0, wallWeight * distFactor) if height - self.r.y < wallDist: distFactor = ((height - self.r.y) - wallDist) / wallDist acc = GGVector(0, wallWeight * distFactor) return acc def getPosition(self): return self.r def getVelocity(self): return self.v def getCenterOfMass(self, distance): center = GGVector() count = 0 for p in birdPositions: dist = p.sub(self.r) d = dist.magnitude() if d < distance: center = center.add(p) count += 1 if count != 0: return center.mult(1.0/count) else: return center def getAverageVelocity(self, distance): avg = GGVector() count = 0 for i in range(len(birdPositions)): p = birdPositions[i] if (self.r.x - p.x) * (self.r.x - p.x) + \ (self.r.y - p.y) * (self.r.y - p.y) < distance * distance: avg = avg.add(birdVelocities[i]); count += 1 return avg.mult(1.0/count) def limitSpeed(self): m = self.v.magnitude() if m < minSpeed: self.v = self.v.mult(minSpeed / m) if m > maxSpeed: self.v = self.v.mult(minSpeed / m) def setAcceleration(self): self.a = self.cohesion(cohesionDist).mult(cohesionWeight) self.a = self.a.add(self.separation(separationDist).mult(separationWeight)) self.a = self.a.add(self.alignment(alignmentDist).mult(alignmentWeight)) self.a = self.a.add(self.wallInteraction()) def act(self): self.setAcceleration() self.v = self.v.add(self.a) # new velocity self.limitSpeed() self.r = self.r.add(self.v) # new position self.setDirection(int(math.degrees(self.v.getDirection()))) self.setLocation(Location(int(self.r.x), int(self.r.y))) # =================== global section ================== def populateTrees(number): blockSize = 70 treesPerBlock = 10 for block in range(number // treesPerBlock): x = getRandomNumber(800 // blockSize) * blockSize y = getRandomNumber(600 // blockSize) * blockSize for t in range(treesPerBlock): dx = getRandomNumber(blockSize) dy = getRandomNumber(blockSize) addActor(Tree(), Location(x + dx, y + dy)) def generateBirds(number): for i in range(number): addActorNoRefresh(Bird(), getRandomLocation(), getRandomDirection()) onAct() # Initialize birdPositions, birdVelocities def onAct(): global birdPositions, birdVelocities # Update bird positions and velocities birdPositions = [] birdVelocities = [] for b in getActors(Bird): birdPositions.append(b.getPosition()) birdVelocities.append(b.getVelocity()) def getRandomNumber(limit): return randint(0, limit-1) # coupling constants cohesionDist = 100 cohesionWeight = 0.01 alignmentDist = 30 alignmentWeight = 1 separationDist = 30 separationWeight = 0.2 wallDist = 20 wallWeight = 2 maxSpeed = 20 minSpeed = 10 startVelocity = 10 numberTrees = 100 numberBirds = 50 birdPositions = [] birdVelocities = [] makeGameGrid(800, 600, 1, False) registerAct(onAct) setSimulationPeriod(10) setBgColor(makeColor(25, 121, 212)) setTitle("Swarm Simulation") show() populateTrees(numberTrees) generateBirds(numberBirds) doRun() |
MEMO |
The simulation is dependent on several coupling constants that determine the "strength" of the interaction. Their values are very sensitive and you may eventually need to adjust them to the performance of your computer. Again, the callback onAct() is activated using registerAct() so that it is automatically called in every simulation cycle. The birds are moved with the method act() of the class bird. |
EXERCISES |
|
ADDITIONAL MATERIAL |
LIST COMPREHENSION |
|
Lists can be created neatly in Python with a special notation. It is based on mathematical notation from set theory
Use the console to test the Python expressions. You can copy them from the table and paste them into the console
|