11.1 FUN MIND GAMES
![]()
INTRODUCTION |
Mind games with mathematical backgrounds are very popular and wide-spread. The goal of this chapter is not to spoil your pleasure of solving such puzzles "by hand" using paper and pen. Much rather, you should experience that the computer can find the solution by solving systematically using backtracking, however, with two significant differences. On the one hand, if no other limitations and strategies are incorporated into the solution process, the solution can take an enormous amount of time, even on a fast computer. On the other hand, the computer can basically find all solutions which may be very difficult to do by hand. This makes it possible to use the computer to provide evidence that a certain solution is the simplest (shortest). |
SUDOKU |
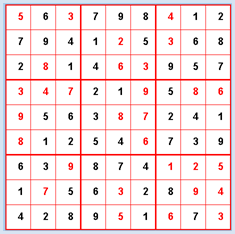
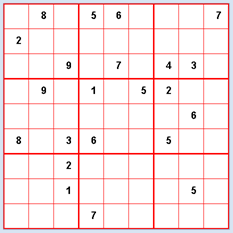
The game Sudoku has boomed and spread ever since 1980, and today it is very popular. You can find them in the puzzle section of many different daily and weekly newspapers. They work like a typical number puzzle with simple rules. In the standard version, the numbers 1 to 9 must be placed in a 9x9 grid so that every number appears exactly once in each row and each column. In addition, the grid is divided into 9 sub-grids with 3x3 cells where the numbers have to occur exactly once. At the beginning of the game, a certain number of cells are already occupied. With an ideal initial situation there should be only one solution. Depending on the initial situation, the puzzle can be easier or more difficult to solve. An experienced Sudoku player uses certain well-known or personal strategies to solve the game. When backtracking with the computer, open cells are systematically one by one filled with numbers from 1 to 9, so that there is no conflict with the rules of the game. If there is no possibility anymore, the last turn is cancelled.
startState = [ \ As usual, you will develop the program step by step. Your first task is to display the game state in the GameGrid and give the user the ability to assign the empty cells with a mouse click. While this is unnecessary in the automatic search of the solution, it allows you to interactively influence the game, which can be especially helpful in the testing phase. Also, this way you can solve the puzzle on the screen instead of on a piece of paper. from gamegrid import * def pressEvent(e): loc = toLocationInGrid(e.getX(), e.getY()) if loc in fixedLocations: setStatusText("Location fixed") return x = loc.x y = loc.y value = startState[y][x] value = (value + 1) % 10 startState[y][x] = value showState(startState) def showState(state): removeAllActors() for y in range(9): for x in range(9): loc = Location(x, y) value = state[y][x] if value != 0: if loc in fixedLocations: c = Color.black else: c = Color.red digit = TextActor(str(value), c, Color.white, Font("Arial", Font.BOLD, 20)) addActorNoRefresh(digit, loc) refresh() makeGameGrid(9, 9, 50, Color.red, False, mousePressed = pressEvent) show() setTitle("Sudoku") setBgColor(Color.white) getBg().setLineWidth(3) getBg().setPaintColor(Color.red) for x in range(4): getBg().drawLine(150 * x, 0, 150 * x, 450) for y in range(4): getBg().drawLine(0, 150 * y, 450, 150 * y) startState = [ [0, 6, 0, 7, 9, 8, 0, 1, 2], [7, 9, 4, 1, 0, 5, 0, 6, 8], [2, 0, 1, 4, 0, 0, 9, 5, 7], [0, 0, 0, 2, 1, 0, 5, 0, 0], [0, 5, 6, 3, 0, 0, 2, 4, 1], [0, 1, 2, 5, 4, 0, 7, 3, 9], [6, 3, 0, 8, 7, 4, 0, 0, 0], [1, 0, 5, 6, 0, 2, 8, 0, 0], [4, 2, 8, 9, 0, 1, 0, 7, 0]] fixedLocations = [] for x in range(9): for y in range(9): if startState[y][x] != 0: fixedLocations.append(Location(x, y)) showState(startState) Highlight program code
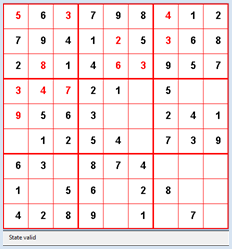
from gamegrid import * def pressEvent(e): loc = toLocationInGrid(e.getX(), e.getY()) if loc in fixedLocations: setStatusText("Location fixed") return xs = loc.x // 3 ys = loc.y // 3 x = loc.x % 3 y = loc.y % 3 value = startState[ys][xs][y][x] value = (value + 1) % 10 startState[ys][xs][y][x] = value showState(startState) if isValid(startState): setStatusText("State valid") else: setStatusText("Invalid state") def showState(state): removeAllActors() for ys in range(3): for xs in range(3): for y in range(3): for x in range(3): loc = Location(x + 3 * xs, y + 3 * ys) value = state[ys][xs][y][x] if value != 0: if loc in fixedLocations: c = Color.black else: c = Color.red digit = TextActor(str(value), c, Color.white, Font("Arial", Font.BOLD, 20)) addActorNoRefresh(digit, loc) refresh() def isValid(state): # Check lines for ys in range(3): for y in range(3): line = [] for xs in range(3): for x in range(3): value = state[ys][xs][y][x] if value > 0 and value in line: return False else: line.append(value) # Check rows for xs in range(3): for x in range(3): row = [] for ys in range(3): for y in range(3): value = state[ys][xs][y][x] if value > 0 and value in row: return False else: row.append(value) # Check subgrids for ys in range(3): for xs in range(3): subgrid = state[ys][xs] square = [] for y in range(3): for x in range(3): value = subgrid[y][x] if value > 0 and value in square: return False else: square.append(value) return True makeGameGrid(9, 9, 50, Color.red, False, mousePressed = pressEvent) show() setTitle("Sudoku") addStatusBar(30) visited = [] setBgColor(Color.white) getBg().setLineWidth(3) getBg().setPaintColor(Color.red) for x in range(4): getBg().drawLine(150 * x, 0, 150 * x, 450) for y in range(4): getBg().drawLine(0, 150 * y, 450, 150 * y) stateWiki = [[[[0, 3, 0], [0, 0, 0], [0, 0, 8]], [[0, 0, 0], [1, 9, 5], [0, 0, 0]], [[0, 0, 0], [0, 0, 0], [0, 6, 0]]], [[[8, 0, 0], [4, 0, 0], [0, 0, 0]], [[0, 6, 0], [8, 0, 0], [0, 2, 0]], [[0, 0, 0], [0, 0, 1], [0, 0, 0]]], [[[0, 6, 0], [0, 0, 0], [0, 0, 0]], [[0, 0, 0], [4, 1, 9], [0, 0, 0]], [[2, 8, 0], [0, 0, 5], [0, 7, 0]]]] startState = stateWiki fixedLocations = [] for xs in range(3): for ys in range(3): for x in range(3): for y in range(3): if startState[ys][xs][y][x] != 0: fixedLocations.append(Location(x + 3 * xs, y + 3 * ys)) showState(startState) Highlight program code
For the backtracking, you have to determine the subsequent nodes of a state with the function getNeighbours(state). For this, you choose an empty cell with getEmptyCell() and insert all numbers in order which belong to a legal game state. At least one of them will be the correct one. In getNeighbours(state), you first copy the given state list into a clone, since you are not allowed to overwrite the state received as a parameter. Then, you fill the empty cells successively with the numbers 1 to 9 and add copies of the allowed states into the neighbor list, which you then finally return [more... A clone is created which the function deepCopy() from module copy].You can adopt the recursively defined function search(), which performs the actual backtracking, almost without changing anything from other backtracking problems. In this case, you are looking for just a single solution and you end the recursive call with the flag found.
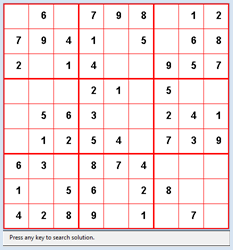
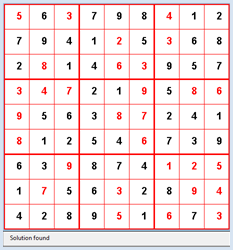
from gamegrid import * def pressEvent(e): loc = toLocationInGrid(e.getX(), e.getY()) if loc in fixedLocations: setStatusText("Location fixed") return x = loc.x y = loc.y value = startState[y][x] value = (value + 1) % 10 startState[y][x] = value showState(startState) if isValid(startState): setStatusText("State valid") else: setStatusText("Invalid state") def getBlockValues(state, x, y): return [state[y][x], state[y][x + 1], state[y][x + 2], state[y + 1][x], state[y + 1][x + 1], state[y + 1][x + 2], state[y + 2][x], state[y + 2][x + 1], state[ y + 2][x + 2]] def showState(state): removeAllActors() for y in range(9): for x in range(9): loc = Location(x, y) value = state[y][x] if value != 0: if loc in fixedLocations: c = Color.black else: c = Color.red digit = TextActor(str(value), c, Color.white, Font("Arial", Font.BOLD, 20)) addActorNoRefresh(digit, loc) refresh() def isValid(state): # Check lines for y in range(9): values = [] for x in range(9): value = state[y][x] if value > 0 and value in values: return False else: values.append(value) # Check rows for x in range(9): values = [] for y in range(9): value = state[y][x] if value > 0 and value in values: return False else: values.append(value) # Check blocks for yblock in range(3): for xblock in range(3): values = [] li = getBlockValues(state, 3 * xblock, 3 * yblock) for value in li: if value > 0 and value in values: return False else: values.append(value) return True def getEmptyCell(state): emptyCells = [] for y in range(9): for x in range(9): if state[y][x] == 0: return [x, y] return [] def cloneState(state): li = [] for y in range(9): line = [] for x in range(9): line.append(state[y][x]) li.append(line) return li def getNeighbours(state): clone = cloneState(state) cell = getEmptyCell(state) validStates = [] for value in range(1, 10): clone[cell[1]][cell[0]] = value if isValid(clone): validStates.append(cloneState(clone)) return validStates def search(state): global found, solution if found: return visited.append(state) # state marked as visited # Check for solution if getEmptyCell(state) == []: solution = state found = True return for neighbour in getNeighbours(state): if neighbour not in visited: # Check if already visited search(neighbour) # recursive call visited.pop() makeGameGrid(9, 9, 50, Color.red, False, mousePressed = pressEvent) show() setTitle("Sudoku") addStatusBar(30) visited = [] setBgColor(Color.white) getBg().setLineWidth(3) getBg().setPaintColor(Color.red) for x in range(4): getBg().drawLine(150 * x, 0, 150 * x, 450) for y in range(4): getBg().drawLine(0, 150 * y, 450, 150 * y) startState = [ [0, 6, 0, 7, 9, 8, 0, 1, 2], [7, 9, 4, 1, 0, 5, 0, 6, 8], [2, 0, 1, 4, 0, 0, 9, 5, 7], [0, 0, 0, 2, 1, 0, 5, 0, 0], [0, 5, 6, 3, 0, 0, 2, 4, 1], [0, 1, 2, 5, 4, 0, 7, 3, 9], [6, 3, 0, 8, 7, 4, 0, 0, 0], [1, 0, 5, 6, 0, 2, 8, 0, 0], [4, 2, 8, 9, 0, 1, 0, 7, 0]] fixedLocations = [] for x in range(9): for y in range(9): if startState[y][x] != 0: fixedLocations.append(Location(x, y)) showState(startState) setStatusText("Press any key to search solution.") getKeyCodeWait(True) setStatusText("Searching. Please wait...") found = False solution = None search(startState) if solution != None: showState(solution) setStatusText("Solution found") else: setStatusText("No solution") Highlight program code
|
MEMO |
|
You can also use Sudokus that you find on the Internet or in a puzzle section. If you have enough patience, your program should always be able to find a solution. You can greatly reduce the computation time if you include the solution strategies that you would also use when solving by hand. It is up to you to improve the algorithm with such heuristic processes. The process that you use to solve the Sudoku can also be applied to Sudoku puzzles that have non-square cells. For this, you only need to adjust the function getBlockValues() accordingly. |
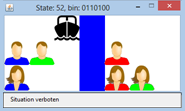
THE JEALOUS HUSBANDS |
"Three jealous husbands find themselves with their wives at a river crossing in the evening where they find a boat without a boatman. The boat is so small that it only fits two people. This poses the question of how all six people can cross the river without ever putting one of the women in the presence of one or two men without her own husband being present, on either side of the land or in the boat." You again solve this problem step by step. First you create the user interface (a GameGrid works well for this) since the people can be easily represented by sprite images. Add the GameGrid actors to an invisible 7x3 grid so that you can draw a river on the middle strip. Since it is only really important if a person is to the left or the right of the river, a binary number is suitable as a data structure where each bit belongs to a particular person. The bit value 0 means that the person is on the left side of the river, and the value 1 means that they are on the right side. Use the bit with the highest value for the boat. In the simulation program there is a blue, a green, and a red couple that you related to the digits of the binary number as follows:
b0 is the bit with the smallest value. If you interpret the state in the decimal system, all numbers between 0 and 127 occur, i.e. there are 128 different states.
You already build a test here with isStateAllowed(state) to check if the current situation is legal according to the rules. (You could also first create a prototype without this test.) from gamegrid import * def pressEvent(e): global state loc = toLocationInGrid(e.getX(), e.getY()) if loc in left_locations: actor = getOneActorAt(loc) if actor != None: x = 6 - actor.getX() y = actor.getY() actor.setLocation(Location(x, y)) if loc in right_locations: actor = getOneActorAt(loc) if actor != None: x = 6 - actor.getX() y = actor.getY() actor.setLocation(Location(x, y)) state = 0 for i in range(7): loc = right_locations[i] actor = getOneActorAt(loc) if actor != None: state += 2**(6 - i) showState(state) def stateToString(state): return str(bin(state)[2:]).zfill(7) def showState(state): sbin = stateToString(state) for i in range(7): if sbin[i] == "0": actors[i].setLocation(left_locations[i]) else: actors[i].setLocation(right_locations[i]) setTitle("State: " + str(state) + ", bin: " + stateToString(state)) if isStateAllowed(state): setStatusText("Situation allowed") else: setStatusText("Situation not allowed") refresh() def isStateAllowed(state): print state stateStr = stateToString(state) mred = stateStr[1] == "1" fred = stateStr[2] == "1" mgreen = stateStr[3] == "1" fgreen = stateStr[4] == "1" mblue = stateStr[5] == "1" fblue = stateStr[6] == "1" if mred and not fred or not mred and fred: # mred/fred not together if not fred and (not mgreen or not mblue) or fred and (mgreen or mblue): return False if mgreen and not fgreen or not mgreen and fgreen:#mgreen/fgreen not together if not fgreen and (not mred or not mblue) or fgreen and (mred or mblue): return False if mblue and not fblue or not mblue and fblue: # mblue/fblue not together if not fblue and (not mred or not mgreen) or fblue and (mred or mgreen): return False return True makeGameGrid(7, 3, 50, None, False, mousePressed = pressEvent) setBgColor(Color.white) addStatusBar(30) show() actors = [Actor("sprites/boat.png"), Actor("sprites/man_0.png"), Actor("sprites/woman_0.png"), Actor("sprites/man_1.png"), Actor("sprites/woman_1.png"), Actor("sprites/man_2.png"), Actor("sprites/woman_2.png")] left_locations = [Location(2, 0), Location(2, 1), Location(2, 2), Location(1, 1), Location(1, 2), Location(0, 1), Location(0, 2)] right_locations = [Location(4, 0), Location(4, 1), Location(4, 2), Location(5, 1), Location(5, 2), Location(6, 1), Location(6, 2)] for i in range(7): addActorNoRefresh(actors[i], left_locations[i]) for i in range(3): getBg().fillCell(Location(3, i), Color.blue) refresh() startState = 0 showState(startState) Highlight program code
In the next step you implement the backtracking algorithm, as you know it from chapter 10.3. Again, you first have to determine all possible successive states for a given state in getNeighbours(state). You begin as follows: First you distinguish whether the boat is located on the left side of the river (state < 64) or the right (state >=64). Then you determine all people who are available to move across the river either as an individual or in a two person team from the lists li_one and li_two. When using removeForbiddenTransfers() you also must consider that a woman can never be in the boat with a man that is not her husband. You implement the backtracking in its familiar form in search(). You copy the solutions into a list named solutions, so that you can access them at the end of the search process to examine the solutions. Thereby you first write out the number of found solutions and then select the shortest one which can then be run through using key press. from gamegrid import * import itertools def pressEvent(e): global state loc = toLocationInGrid(e.getX(), e.getY()) if loc in left_locations: actor = getOneActorAt(loc) if actor != None: x = 6 - actor.getX() y = actor.getY() actor.setLocation(Location(x, y)) if loc in right_locations: actor = getOneActorAt(loc) if actor != None: x = 6 - actor.getX() y = actor.getY() actor.setLocation(Location(x, y)) state = 0 for i in range(7): loc = right_locations[i] actor = getOneActorAt(loc) if actor != None: state += 2**(6 - i) setTitle("State: " + str(state) + ", bin: " + stateToString(state)) if isStateAllowed(state): setStatusText("Situation allowed") else: setStatusText("Situation not allowed") refresh() def stateToString(state): return str(bin(state)[2:]).zfill(7) def showState(state): sbin = stateToString(state) for i in range(7): if sbin[i] == "0": actors[i].setLocation(left_locations[i]) else: actors[i].setLocation(right_locations[i]) refresh() def getTransferInfo(state1, state2): state1 = state1 & 63 state2 = state2 & 63 mod = state1 ^ state2 passList = [] for n in range(6): if mod % 2 == 1: if n // 2 == 0: couple = "blue" elif n // 2 == 1: couple = "green" elif n // 2 == 2: couple = "red" if n % 2 == 0: passList.append("f" + couple) else: passList.append("m" + couple) mod = mod // 2 return passList def getTransferSequence(solution): transferSequence = [] oldState = solution[0] for state in solution[1:]: transferSequence.append(getTransferInfo(oldState, state)) oldState = state return transferSequence def isStateAllowed(state): stateStr = stateToString(state) mred = stateStr[1] == "1" fred = stateStr[2] == "1" mgreen = stateStr[3] == "1" fgreen = stateStr[4] == "1" mblue = stateStr[5] == "1" fblue = stateStr[6] == "1" if mred and not fred or not mred and fred: # mred/fred not together if not fred and (not mgreen or not mblue) or fred and (mgreen or mblue): return False if mgreen and not fgreen or not mgreen and fgreen:#mgreen/fgreen not together if not fgreen and (not mred or not mblue) or fgreen and (mred or mblue): return False if mblue and not fblue or not mblue and fblue: # mblue/fblue not together if not fblue and (not mred or not mgreen) or fblue and (mred or mgreen): return False return True def removeForbiddenTransfers(li): forbiddenPairs = [(0, 3), (0, 5), (1, 2), (2, 5), (1, 4), (3, 4)] allowedPairs = [] for pair in li: if pair not in forbiddenPairs: allowedPairs.append(pair) return allowedPairs def getNeighbours(state): neighbours = [] li_one = [] # one person in boat bin = stateToString(state) if state < 64: # boat at left for i in range(6): if bin[6 - i] == "0": li_one.append(i) li_two = list(itertools.combinations(li_one, 2)) #two persons in boat li_two = removeForbiddenTransfers(li_two) else: # boat at right for i in range(6): if bin[6 - i] == "1": li_one.append(i) li_two = list(itertools.combinations(li_one, 2)) li_two = removeForbiddenTransfers(li_two) li_values = [] if state < 64: # boat at left, restrict to two persons transfer for li in li_two: li_values.append(2**li[0] + 2**li[1] + 64) else: # boat at right, one or two persons transfer for i in li_one: li_values.append(2**i + 64) for li in li_two: li_values.append(2**li[0] + 2**li[1] + 64) for value in li_values: v = state ^ value if isStateAllowed(v): # restrict to allowed states neighbours.append(v) return neighbours def search(state): visited.append(state) # state marked as visited # Check for solution if state == targetState: solutions.append(visited[:]) for neighbour in getNeighbours(state): if neighbour not in visited: # Check if already visited search(neighbour) # recursive call visited.pop() nbSolution = 0 makeGameGrid(7, 3, 50, None, False, mousePressed = pressEvent) addStatusBar(30) setBgColor(Color.white) setTitle("Searching...") show() visited = [] actors = [Actor("sprites/boat.png"), Actor("sprites/man_0.png"), Actor("sprites/woman_0.png"), Actor("sprites/man_1.png"), Actor("sprites/woman_1.png"), Actor("sprites/man_2.png"), Actor("sprites/woman_2.png")] left_locations = [Location(2, 0), Location(2, 1), Location(2, 2), Location(1, 1), Location(1, 2), Location(0, 1), Location(0, 2)] right_locations = [Location(4, 0), Location(4, 1), Location(4, 2), Location(5, 1), Location(5, 2), Location(6, 1), Location(6, 2)] for i in range(7): addActorNoRefresh(actors[i], left_locations[i]) for i in range(3): getBg().fillCell(Location(3, i), Color.blue) refresh() startState = 0 targetState = 127 solutions = [] search(startState) maxLength = 0 maxSolution = None minLength = 100 minSolution = None for solution in solutions: if len(solution) > maxLength: maxLength = len(solution) maxSolution = solution if len(solution) < minLength: minLength = len(solution) minSolution = solution setStatusText("#Solutions: " + str(len(solutions)) + ", Min Length: " + str(minLength) + ", Max Length: " + str(maxLength)) setTitle("Press key to cycle") oldState = startState for state in minSolution[1:]: getKeyCodeWait(True) showState(state) info = getTransferInfo(oldState, state) setTitle("#Transferred: " + str(info)) oldState = state setTitle("Done. #Boat Transfers: " + str((len(minSolution) - 1))) Highlight program code
|
MEMO |
|
Puzzles of this type have the feature that you do not know whether they have exactly one or multiple solutions from the start. It turns out that it is much easier for us humans to find a solution, than it is to prove that there is no solution. For the computer which systematically searches for all solutions with an exhaustive search, the search for all solutions is generally not a problem except that it can take a long time. This is unfortunately already the case with relatively simple games, due to combinatorial explosion, so we again bump into the limits of using the computer. |
EXERCISES |
|